集合の世界

　私の研究分野では、すべてのものが集合であるところの世界を考え、集合と集合の間の要素関係を使って、その世界の事実関係を記述する。例えば、どのような集合の世界であっても、集合xはx自身の要素ではないこ とは、事実と考える。
　この世界では、ツェルメロ-フレンケルの公理と選択公理を合わせた公理系(ZFC)によって、期待される標準的な事実が言い表される。また、自然数0,1,2,...、整数、有理数、実数、ユークリッド空間、関係、関数、関数空間にあたるものが構成でき、数学的事実を論ずることができる。つまり、どの集合の世界においても一般的に考えられている数学を論ずることができるのである。よってここに、『集合の世界に依存して数学的事実が異なりはしないか』という、疑問なり期待が生じてくることとなる。

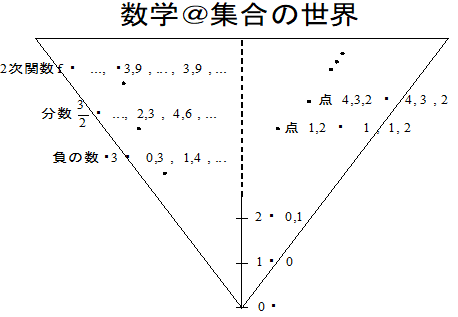
　では、このことに関して任意の集合の世界の内側で少し考察してみよう。集合x から要素関係で推移的に到達可能な集合の全体TC(x)を考える。TC(x)が有限集合である x の全体をAとする。Aは有限の世界を映し出すと考えられる。次に、TC(x)が高々可算集合であるx の全体をBとする。AはBの要素になる。つまり、BはAに比べ、かなり大きな世界であると言える。一般に、集合の世界自体を要素とする集合の世界が存在すると言えるのである。
　ところで、集合の世界を構成するには「閉じていること」が要請される。任意の集合の世界に対し、自身と見分けがつかない真部分な世界が構成できる（レーベンハイム-スコーレムの定理）。また、集合の世界 Vと、Vの外に存在する集合Gとで、「閉じている」集合の世界V[G]を構成する方法が　1960年代 コーエンにより、編み出された。これにより、連続体仮説について、V[G]のあるものは満たし、あるものはその否定を満たすことが示された。この事実は、ある種の数学的事実が集合の世界に依存する事を示している。
　結論として、ZFCが無矛盾である限り、連続体仮説、およびその否定のどちらもZFCでは証明不可能である。現在、VからV[G]への拡張にあたることを無数回繰り返すなど、さまざまな目的で集合の世界を拡張して見せる研究が、進行中である。