トップ>R
Rについて
Rは高機能な統計処理ソフトです(しかも無償!)。
Rの詳細についてはRjpWikiを、インストール方法については数量的アプローチ講義資料①(R)、講義資料②(RStudio)をどうぞ。Windowsでインストーラーの指示通りにインストールすると、OneDriveが邪魔してパッケージがうまくインストールできないなど不具合が出ることがあるので、インストール先を少し変えています。Macの人は気にせず、インストーラーの指示どおりにインストールすればいいはずです。
RjpWikiが機能していないので、Rを取得する場合は、以下からダウンロードしてください。
Rを使いやすくするためのインターフェイスには以下のものがあります。
Rでの分析の前に
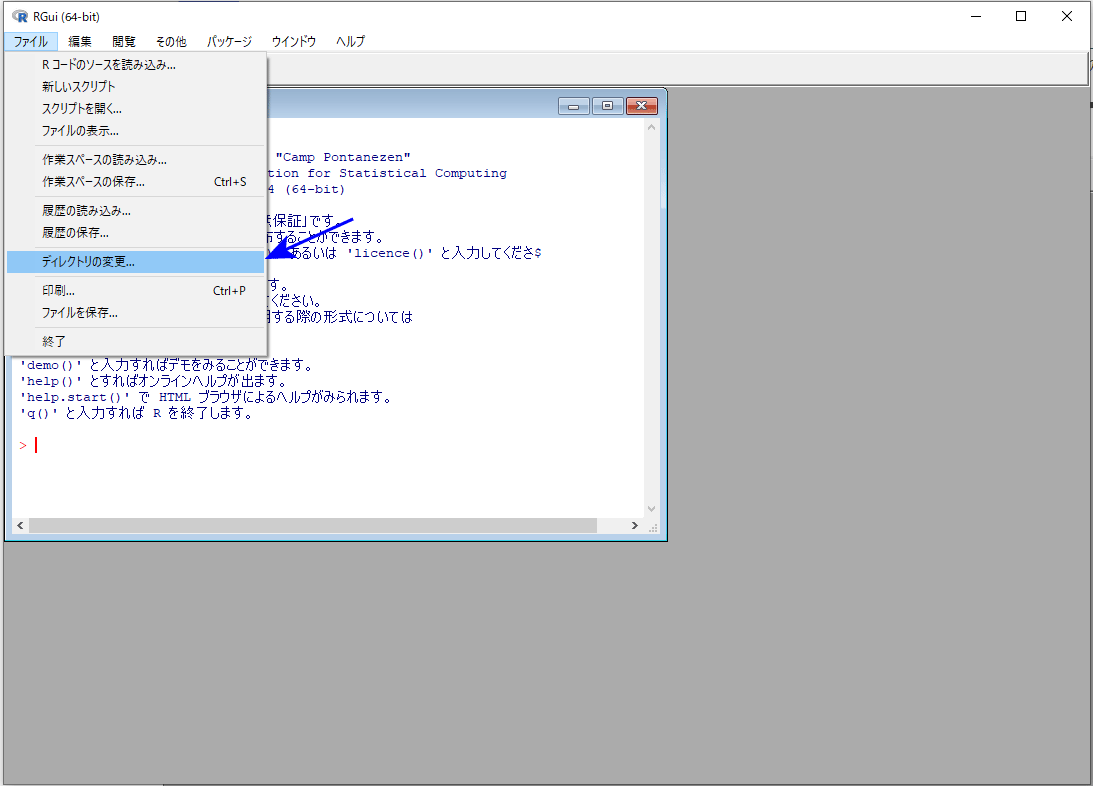
Rで分析するにあたって、作業場(データファイル等の置き場所)を指定する必要があります。「ファイル」→「ディレクトリの変更...」と進んでフォルダを指定します。Macの場合は、「その他」→「作業ディレクトリの変更」でフォルダを指定します。
以下のようなコマンドを実行して作業場を指定することもできます。これは、デスクトップに「Rdata」というフォルダがある場合です。ユーザー名は各自のものになります。
> setwd("c:/Users/ユーザー名/Desktop/Rdata")
Macの場合は以下のようになります。
> setwd("/Users/ユーザー名/Desktop/Rdata")
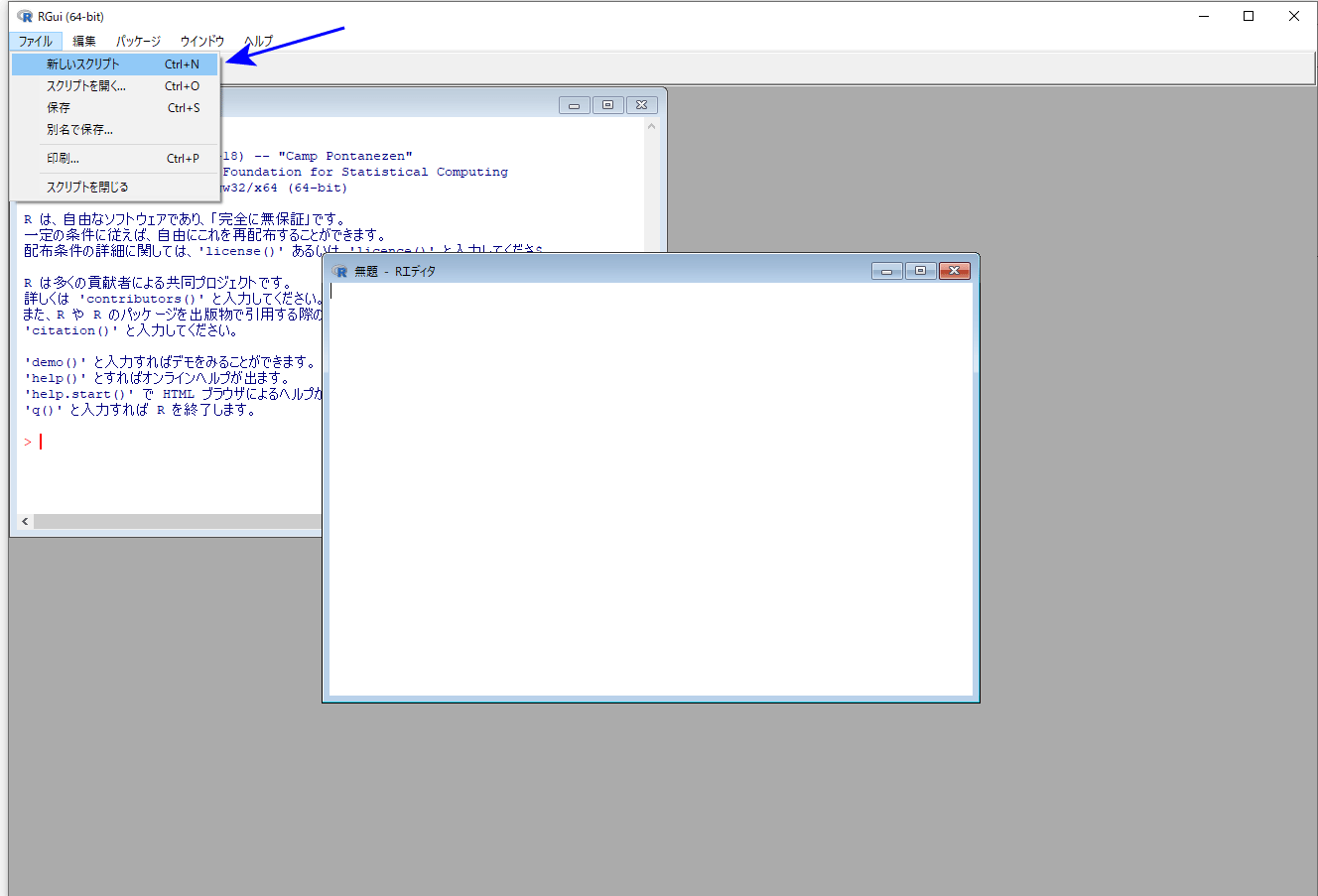
分析にあたっては、コマンドを保存しながら進めるのが効率的です。「ファイル」→「スクリプトを開く...」でRエディタが開くのでそこにコマンドを記述し、実行します。
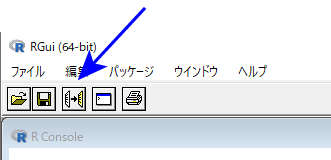
Rエディタ 上でコマンドを実行する場合は、実行したいコマンドのどこかにコマンドプロンプト(点滅している縦線)がある状態で、以下のボタンを押します。または、ショートカット「Ctrl+R」で実行できます。
Rのコマンド
用語
データフレーム:RではCSVファイルなどのデータセットを読み込んで分析しますが、読み込んだデータセットをデータフレームと呼びます。このデータフレームは元のCSVファイルと同じ内容ですが、R専用の別ファイルとなっています。ですので、データフレームを加工しても元のCSVファイルは影響を受けません。
NA:Not Available。欠損値とも呼び、データがないことを意味しています。分析によって、NAのデータを持つ対象は自動的に分析に使われなかったり、エラーになります。
c( ):各コマンドで頻繁に出てくる関数です。基本的には、いくつかの数値や要素をベクトルやリストという一つの単位にまとめる機能を持ちます。combine values into a vector or listのcのようです。
注意
以下のコマンドでは
> attach(data1)
のようにデータフレームの指定を前提としているケースがあります。そのため、そのままコピペして実行すると失敗することがあります。attachを使用しないときは、変数名にデータフレーム名をつけて実行してください(var1→data1$var1)。あるいは受け付けない関数もありますが、使用するデータフレームを指定するのがよいでしょう(data=data1)。
ここに掲載のコマンドは授業の補足のためのメモ書きであり、説明不足な部分が多いです。ご容赦ください。
目次(新しく追加したものが上になっています。)
推定に使用した対象と変数だけで新たにデータフレームを作成する。
パネルデータでidごとに特定のwaveの値をすべてのwaveにコピーする。
Macで漢字(都道府県名など)がデータにあって読み込めないとき
一行目に変数名のないデータを読み込む 一行目に変数名(id、waveなど)がないデータを読み込む場合には、以下のようにヘッダーをFにします。 > data1 <- read.csv("test.csv", header=F)
変数名は自動的に左からV1、V2のようにつけられます。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
推定に使用した対象と変数だけで新たにデータフレームを作成する。 推定に使用した対象で記述統計を計算したい時がありますが、model.frameという関数を使うと、目的の対象だけ残したデータフレームができるようです。まだ使いこなしていないので、とりあえずメモ程度ですが、yとxに欠損値のあるdata1があったとします。 > data1 id y x w 1 1 21 3 1 2 2 34 5 0 3 3 15 1 1 4 4 NA 2 0 5 5 35 4 1 6 6 22 5 0 7 7 18 2 0 8 8 17 NA 0 9 9 31 6 1 10 10 28 4 1 そこでy~xの回帰を行い、使用された対象と変数だけで新たなデータフレームdata2を作成します。
> data2 <- model.frame(y~x, data=data1)
> data2
y x
1 21 3
2 34 5
3 15 1
5 35 4
6 22 5
7 18 2
9 31 6
10 28 4
idとwは推定に使用されなかったので、data2からは落ちていますが、このデータフレームを使って記述統計を計算すれば良いでしょう。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
パネルデータでidごとに特定のwaveの値をすべてのwaveにコピーする。 パネルデータでは、wave1の調査でだけ性別など変わりにくい属性を質問することがあり、wave2以降でデータが欠損していることがあります。ここでは、wave1の値を他のすべてのwaveにコピーする方法を説明します。練習用に個体(id)、時点(wave)、変数(x1)からなるdata1を作成します。 > data1 <- data.frame(id = rep(c(1:3), each = 3), wave = c(1:3), x1 =c(1:9)) > data1 id wave x1 1 1 1 1 2 1 2 2 3 1 3 3 4 2 1 4 5 2 2 5 6 2 3 6 7 3 1 7 8 3 2 8 9 3 3 9 x1について、wave1時点の情報だけを残し、他のwaveの値を-9にした、x1aをdata1に追加します。 > data1$x1a <- ifelse(data1$wave==1, data1$x1, -9) > data1 id wave x1 x1a 1 1 1 1 1 2 1 2 2 -9 3 1 3 3 -9 4 2 1 4 4 5 2 2 5 -9 6 2 3 6 -9 7 3 1 7 7 8 3 2 8 -9 9 3 3 9 -9 パイプ演算子(%>%)を使うために、パッケージdplyrを読み込みます。 > library(dplyr) idごとにx1aの最大値(max)をとる新たな変数x1bを作成し、data1に追加します。 > data1 <- data1 %>% group_by(id) %>% mutate(x1b = max(x1a)) data1を見ると、x1bができているのが確認できます。
> data1
# A tibble: 9 × 5
# Groups: id [3]
id wave x1 x1a x1b
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
パネルデータでラグ付き変数を作成する。 練習用に個体(id)、時点(wave)、変数(x1)からなるdata1を作成します。 > data1 <- data.frame(id = rep(c(1:3), each = 3), wave = c(1:3), x1 =c(1:9)) > data1 id wave x1 1 1 1 1 2 1 2 2 3 1 3 3 4 2 1 4 5 2 2 5 6 2 3 6 7 3 1 7 8 3 2 8 9 3 3 9 パイプ演算子(%>%)を使うために、パッケージdplyrを読み込みます。 > library(dplyr) 2期前の値をとるx2を作成し、data1に追加します。 > data1 <- data1 %>% > group_by(id) %>% > mutate(x2 = lag(x1, n = 2, default = NA)) data1を見ると、x2ができているのが確認できます。
> data1
# A tibble: 9 × 4
# Groups: id [3]
id wave x1 x2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
場合分けで計算式を変えて新しい変数を作成する。 例えば、生年月(ybirth, mbirth)から年齢を計算するとき、4月生まれ以前と5月生まれ以降で計算を変えたいときがあります。その場合、以下のような方法があります。パッケージdplyrとmutate関数を使います。 > library(dplyr) > data2 <- data2%>% > mutate(age1 = ifelse(mbirth<=4, 2007-ybirth, ifelse(mbirth>=5, 2006-ybirth, ybirth))) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
stargazerで複数の推定結果を比較する。 変数の組み合わせでいくつかのモデルを推定して結果を比較したいときがあります。その場合、stargazerを使用するのが便利です。例えば、以下のように2つの結果をreg1、reg2に格納します。 > reg1 <- lm(enr~inc+stu, data=data1) > reg2 <- lm(enr~inc+stu+univ, data=data1) パッケージstargazerを読み込んで、2つの結果を1つの表にまとめます。 > library(stargazer) > stargazer(reg1,reg2,type="text")
なお、初期設定では有意水準は10%が下限となっていますが、以下のように指定することで有意水準を変更できます。これは下限を5%にする場合です。 > stargazer(reg1,reg2,type="text",star.cutoffs=c(0.05,0.01,0.001)) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
条件にあった対象のみで度数分布を確認する あるデータフレーム(data1)で、男性(sexa==1)だけで、配偶状態(marc)の度数分布を確認するには、以下のようにします。 > table(subset(data1,sexa==1,c(marc))) 女性(sexa==2)だけで、最終学歴(educ)の度数分布を確認するには、以下のようにします。 > table(subset(data1,sexa==2,c(educ))) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
いくつかの自由度(k)で見たカイ2乗分布のグラフ 自由度が大きくなると分布が右へ移動するのがわかります。 > curve(dchisq(x,1),0,30,col="red",ylab="f(x)",family="serif") > curve(dchisq(x,2),0,30,add=TRUE,col="blue") > curve(dchisq(x,5),0,30,add=TRUE,col="green") > curve(dchisq(x,10),0,30,add=TRUE) > abline(h=0) > text(2,0.6,labels="k=1",family="serif") > text(2.6,0.29,labels="k=2",family="serif") > text(4,0.18,labels="k=5",family="serif") > text(10,0.12,labels="k=10",family="serif") 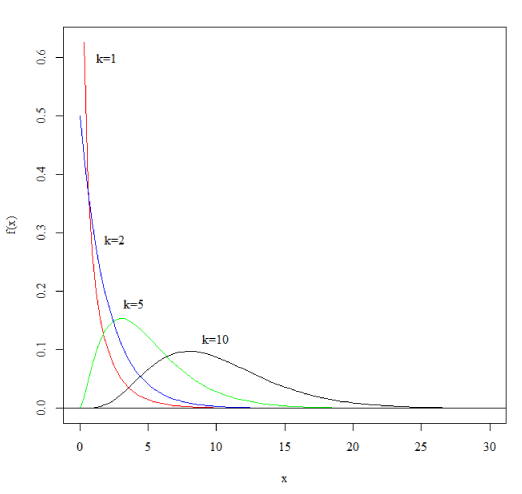 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
平均は異なるが等分散の正規分布のグラフ 平均0、分散1の正規分布(青)と平均1、分散1の正規分布(緑)のグラフを表示する。 > curve(dnorm(x,0,1),-6,6, ylim=c(0,0.5), ylab="", col="blue") > curve(dnorm(x,1,1),-6,6, ylim=c(0,0.5), ylab="", col="green", add=TRUE) > segments(qnorm(0.5,0,1), 0, qnorm(0.5,0,1), dnorm(qnorm(0.5,0,1),0,1)) > segments(qnorm(0.5,1,1), 0, qnorm(0.5,1,1), dnorm(qnorm(0.5,1,1),1,1)) > abline(h=0) 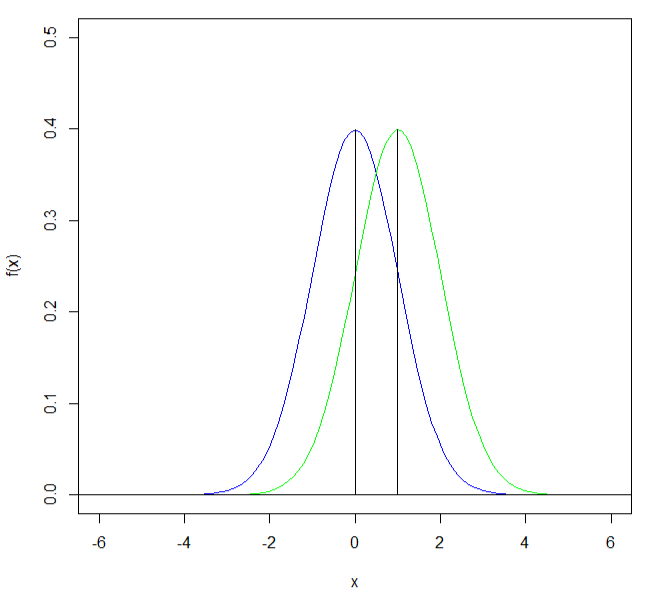 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Macでグラフを作成する際、ラベルに漢字を表示させたいとき Macでグラフに日本語を表示させたいときに□□□のようになってしまうことがあります。この場合、以下のようにpar()で使用フォントを設定すれば表示できるようになります。フォントはいくつか選択肢があります(HiraginoSans-W3, HiraMaruProN-W4, HirakakuProN-W3)。日本語以外の数字の部分も同じフォントになります。 > par(family= "HiraKakuProN-W3") > plot(data$inc,data1$col,xlab="県民所得(千円)", ylab="大学進学率(%)") |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Macで漢字(都道府県名など)がデータにあって読み込めないとき 読み込むデータに日本語が入っている場合、Macでは以下のようなエラーが出ます。
> data1 <- read.csv("educ2.csv")
type.convert.default(data[[i]], as.is = as.is[i], dec = dec, でエラー:
'<96>k<8a>C<93><b9>' に不正なマルチバイト文字があります
そこで読み込みコマンドにオプション(fileEncoding)を追加します。
> data1 <- read.csv("educ2.csv", fileEncoding="CP932")
> data1
pref inc enr stu univ cpi
1 北海道 2476 40.4 12.6 0.65 99.3
2 青森 2333 41.9 12.4 0.73 99.8
3 岩手 2309 41.1 12.4 0.38 98.7
(以下略) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
時間データを分に変換する 時間データで「時間.分」という形になっていることがあります。例えば2.54は2時間54分のことであり、2.54時間(約2時間30分)のことを意味しているのではありません。また、2.60~2.99というデータも存在しないので、そのまま使用するとおかしな散布図になります。そこで、分に換算して分析に用いることになります。以下のように関数を利用して換算します。 > floor(2.54)*60+(2.54%%1)*100 [1] 174 floor(x)はxを超えない整数を返す関数で、y%%zの%%は、yをzで割り、その余りを得る演算子です。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
データフレームの指定部分で記述統計量を計算2 並んでいる複数の変数の記述統計の計算コマンドは下(データフレームの指定部分で記述統計量を計算)で説明しましたが、データフレームの離れた複数箇所で記述統計を計算したいときがあります。例えば、以下のデータで2~3列目(inc,enr)と5列目(univ)の記述統計を計算したいとしましょう。 > data1
pref inc enr stu univ cpi
1 北海道 2476 40.4 12.6 0.65 99.3
2 青森 2333 41.9 12.4 0.73 99.8
3 岩手 2309 41.1 12.4 0.38 98.7
(以下略)
以下のようにコマンドします。 > summary(data1[,c(2:3,5)]) > apply(data1[,c(2:3,5)],2,sd) もちろん変数名を指定してもできます。 > summary(data1[,c("inc","enr","univ")])
> apply(data1[,c("inc","enr","univ")],2,sd)
なお、データフレームの2~3列目と5列目だけコンソールに表示させたい時は以下のとおりです。 > data1[,c(2:3,5)] |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
複数回答のデータからある選択肢該当ダミーを作成する 複数回答(あてはまるものに○系の設問)のデータで、選んだ選択肢の番号が1変数に1つずつ入っていることがあります。例えば、転職の理由として該当するもの3つに〇をするような場合です。以下は、5人が8つの選択肢から選んだものがq1_1~q1_3に入っています。1つだけ選んだ人もいれば3つ選んだ人もいます。 > data1 q1_1 q1_2 q1_3 1 1 2 3 2 3 5 . 3 2 . . 4 1 4 8 5 2 3 . ここから、選択肢3を選んだというダミー変数(q1_c3)を作成したいとしましょう。選択肢3を選んだ人を1とする場合、以下のようにコマンドします。「|」は「または(or)」の演算子です。 > data1$q1_c3[data1$q1_1 == 3 | data1$q1_2 ==3 | data1$q1_3 ==3 ] <- 1 > data1 q1_1 q1_2 q1_3 q1_c3 1 1 2 3 1 2 3 5 . 1 3 2 . . NA 4 1 4 8 NA 5 2 3 . 1 該当しない人はNAになっているので0にリコードしておきましょう。パッケージcarを読み込んでから、リコードします。 > library(car) > data1$q1_c3 <- recode(data1$q1_c3, '1=1;NA=0') > data1 q1_1 q1_2 q1_3 q1_c3 1 1 2 3 1 2 3 5 . 1 3 2 . . 0 4 1 4 8 0 5 2 3 . 1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
複数の変数から1つの新しい変数をつくる 2つの変数の回答の組み合わせで新しい変数をつくりたい場合があります。以下のようなx1とx2の2つの変数があったとしましょう。 > data1 x1 x2 1 1 1 2 2 1 3 1 2 4 2 2 5 2 1 例えばx1が1かつx2が1の場合に1、x1が1かつx2が2の場合に2、x1が2かつx2が1の場合に3、x1が2かつx2が2の場合に4、となる新しい変数(x3)を作成するには以下のようにコマンドします。 > data1$x3[data1$x1==1 & data1$x2==1] <- 1 > data1$x3[data1$x1==1 & data1$x2==2] <- 2 > data1$x3[data1$x1==2 & data1$x2==1] <- 3 > data1$x3[data1$x1==2 & data1$x2==2] <- 4 > data1 x1 x2 x3 1 1 1 1 2 2 1 3 3 1 2 2 4 2 2 4 5 2 1 3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
datファイルの読み込み データファイルがxxx.datのように拡張子がdatになっている場合、以下のようにコマンドして読み込みます。 > data1 <- read.delim("xxx.dat") なお、datファイルではデータがタブで区切られています。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
データフレームの指定部分で記述統計量を計算 summary関数では標準偏差(sd)を計算してくれないので別途、計算する必要があります。ここではapply関数を利用して、複数の変数の標準偏差を一度に計算してみます。 > apply(data1[,2:3],2,sd)
inc enr
378.681617 7.188327
apply関数の第1引数でデータフレームdata1の2列目から3列目を指定しています。[行,列]で場所をしています。第2引数で列単位で計算するよう指定しています。第3引数で計算する統計量をsd(標準偏差)に指定しています。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2次関数による推定 独立変数に2次項を入れて推定したい場合、以下のように2次項を新たな変数として作成してモデルに入れます。例えば年齢(age)の2次項を使った推定をしたい場合は以下のようにします。 > data1$age2 <- data1$age^2 > lm(inc~age+age2, data=data1) あるいは、I()関数を使うと2次項をデータフレームに追加することなく推定できます。 > lm(inc~age+I(age^2), data=data1) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Logitモデルの限界効果とオッズ比 Logitモデルの推定係数をそのまま解釈することは難しいです。そこで限界効果を計算する必要があります。ただし、非線形の回帰分析のため、限界効果を見たい独立変数およびその他の独立変数の水準(値)によって限界効果が異なります。 あらかじめmfxパッケージをインストールしておき、呼び出します。 > library(mfx) 平均的な限界効果(独立変数に実際の値を使い、各対象で限界効果を計算し推定サンプルで平均化したもの)を求める場合は > logitmfx(Y~X1+X2+X3, data=data1, atmean=F) 平均値での限界効果(独立変数に平均値を代入して計算したもの)を求める場合は > logitmfx(Y~X1+X2+X3, data=data1) また、社会学等ではオッズ比が使われることが多いので参考までに。 > logitor(Y~X1+X2+X3, data=data1) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Rの出力をExcelに貼り付け Rの出力をそのままExcelに貼り付けると、下の図のように変数名や係数、標準誤差などが1セルにまとめて入ってしまいます。 これらの数値を1セルごとに入れたい場合、「データ」タブの「区切り位置」を押します。
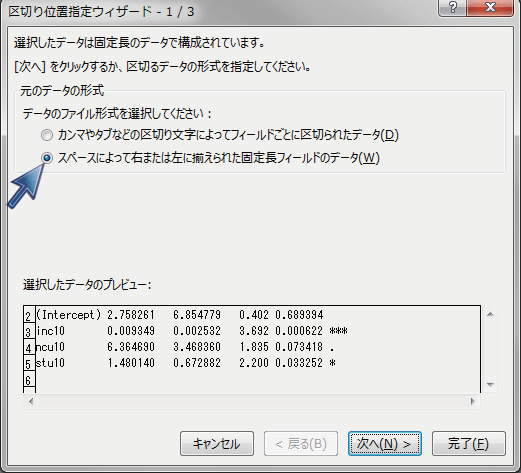
すると、以下のような画面になりますので、「スペースに・・・」が選択されていることを確認して「次へ」を押します。
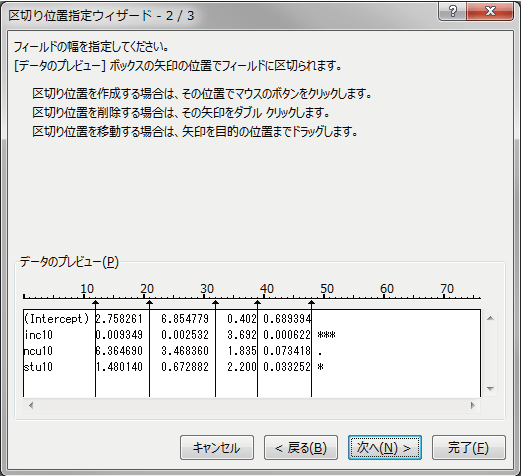
どこで区切るか表示されますので、よければ「次へ」か「完了」を押してください。 次の画面では表示形式を操作できますが、ここでは必要なさそうです。
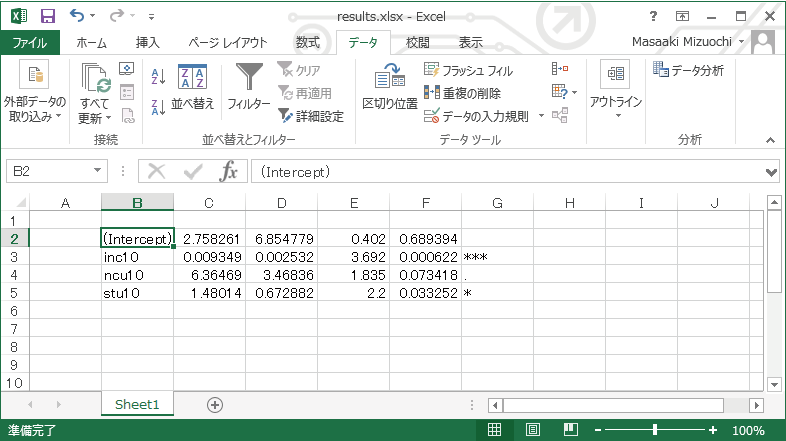
以下のようにきれいにセルに入りました。
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
加工した数値変数が正しく作成されたか並べて確認 例えば数値変数incを10倍してinc10に、incを100倍してinc100を作成し、並べるには以下を実行します。新たな変数の作成方法として、$でデータフレームをした場合とwith関数を使った2つの方法が示してありますが、どちらでもかまいません。with関数は使用するデータフレームをこの命令でだけ指定できます。attach()の場合はdetach()するまでデータフレームを指定し続けるのと対照的です。 > data1$inc10 <- data1$inc*10
> data1$inc100 <- with(data1,inc*100)
> data1[,c("inc","inc10","inc100")]
inc inc10 inc100
1 2476 24760 247600
2 2333 23330 233300
3 2309 23090 230900
(以下略)
因子の場合はクロス表でも確認できます。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
サンプルサイズの確認 順序回帰モデルの推定などでは、使用したデータ数が表示されないことがあります。結果としては保存されているので表示することができます。例えば推定結果がOrdRegModel.1に格納されていたとします。この場合、以下のように入力し実行します。 > OrdRegModel.1$nobs あるいは > OrdRegModel.1$n です。stargazerでも確認できます。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
条件に合うデータだけ抜き出してデータフレームをつくる まずはテストデータを作成します。 > w <- c(0,1,1,0,1,1,0,1) > x <- c(6,8,10,5,7,8,4,3) > y <- c(120,320,430,450,340,210,270,410) > z <- c(1,2,3,2,3,3,2,1) > data <- data.frame(w,x,y,z) > data w x y z 1 0 6 120 1 2 1 8 320 2 3 1 10 430 3 4 0 5 450 2 5 1 7 340 3 6 1 8 210 3 7 0 4 270 2 8 1 3 410 1 subset関数で条件を指定(z==3)し、抜き出す変数を指定(x,y,z)します。 > data1 <- subset(data,z==3,c(x,y,z)) > data1 x y z 3 10 430 3 5 7 340 3 6 8 210 3 zが3のデータだけ抜き出すことができました。 ただし、attachして抜き出そうとしてもエラーになるようです。 > attach(data) > data2 <- subset(z==3,c(x,y,z)) 以下にエラー subset.default(z == 3, c(x, y, z)) : 'subset' は論理値でなければなりません > data2 エラー: オブジェクト 'data2' がありません |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
データの四捨五入 小数部分のあるincという変数について、四捨五入で整数にして、新しい変数incrを作る場合は以下のようにコマンドします。 > data1$incr <- round(data1$inc,digits=0) また、四捨五入してもとのincに上書きしてしまう場合は以下のようにコマンドします。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ベクトルをデータフレームに 以下のように2つのベクトルがあるとします。 > x <- c(1:10) > y <- c(1,8,15,18,22,23,22,24,26,24) これらを1つのデータフレームにまとめるには以下のようにコマンドします。 var1とvar2の変数名は任意です。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
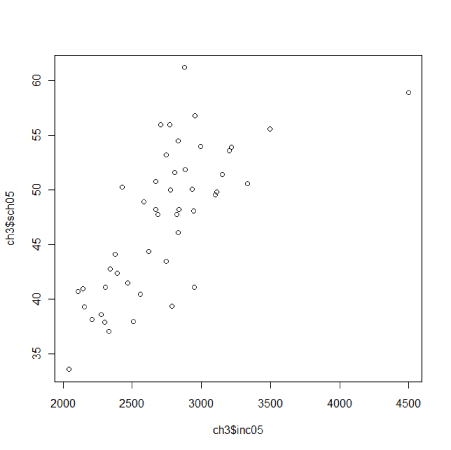
散布図のラベル表示 ここでは都道府県データを使って通常の散布図を描きました。ただし、どのマークがどの都道府県なのかわかりません。 > plot(ch3$inc05,ch3$sch05)
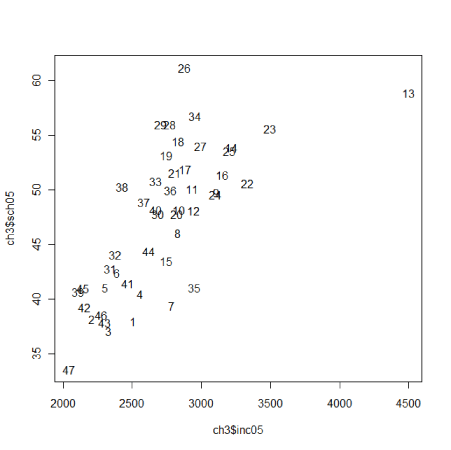
そこで、データの並び番号で表示してみます。 1行目のtype="n"はマークを表示しない命令です。 2行目で並び番号を表示させています。 > plot(ch3$inc05,ch3$sch05,type="n") > text(ch3$inc05,ch3$sch05)
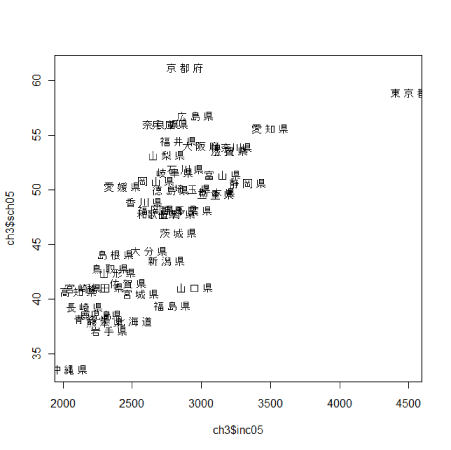
都道府県名を表示したい場合は以下のようにします。 1行目はデータフレームch3の1列目にある都道府県名を抜き出し、labelという名前で保存しています。 3行目でlabelを使用しています。 > label <- ch3[,1] > plot(ch3$inc05,ch3$sch05,type="n") > text(ch3$inc05,ch3$sch05,label)
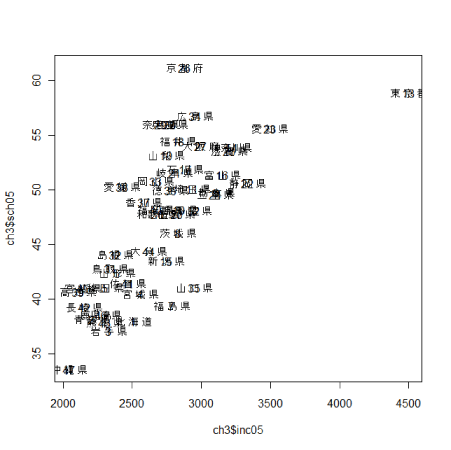
都道府県名は横に広いため、実際のマークの位置との対応を確認します。 上の散布図が表示された状態でさらに以下を実行します。 > text(ch3$inc05,ch3$sch05) 見にくいですが、都道府県名の真ん中にマークがあることがわかります。愛知県であれば「知」がマークということです。 データ上、都道府県名は「愛 知 県」というようになっていますが「愛知」とすれば、もう少しすっきりと表せるでしょう。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
対数 10の自然対数をとるには > log(10) [1] 2.302585 底が2の場合 > log2(10) [1] 3.321928 底が10の場合 > log10(10) [1] 1 ある変数x1の自然対数をとってln_x1として保存する場合 > ln_x1 <- log(x1) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
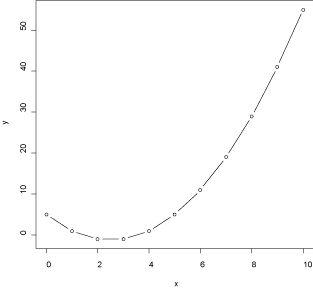
散布図 散布図でポイントを線でつなぐにはtypeで指定します。 まず適当なデータを生成します。 > x <- 0:10 > y <- x^2-5*x+5 > x [1] 0 1 2 3 4 5 6 7 8 9 10 > y [1] 5 1 -1 -1 1 5 11 19 29 41 55 次にplot命令でtypeを指定します。 > plot(x, y, type="b") #線とポイント、重なりなし
そのほかにもいくつかバリエーションがあります。 > plot(x,y,type="l") #線のみ > plot(x,y,type="o") #線とポイント、重なりあり > plot(x,y,type="c") #線のみ、ポイント部分空白 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
データのソート 以下のようなデータフレーム(data1)があるとします。 > data1
pref inc enr
1 北海道 2476 40.4
2 青森 2333 41.9
3 岩手 2309 41.1
4 宮城 2455 45.5
5 秋田 2302 44.5
(略)
43 熊本 2346 43.1
44 大分 2486 47.4
45 宮崎 2228 43.0
46 鹿児島 2401 42.0
47 沖縄 2037 36.7
これを変数incの昇順に並べ替えます。まずorder関数でincの順を作成し、その順を表示してみます。 > sort <- order(data1$inc) > sort [1] 47 39 45 31 5 32 3 2 42 43 6 46 4 41 1 44 29 38 7 20 [21] 33 28 30 21 15 37 17 36 40 19 11 18 10 12 35 27 26 24 14 34 [41] 9 8 16 23 22 25 13 すると上のように当初の都道府県の並び番号で順が示されます。この結果を使って並べ替えたデータフレームを新たに作成し、表示します。 > data1a<-data1[sort,]
> data1a
pref inc enr
47 沖縄 2037 36.7
39 高知 2207 45.4
45 宮崎 2228 43.0
31 鳥取 2234 43.8
5 秋田 2302 44.5
(略)
16 富山 3021 54.2
23 愛知 3073 58.9
22 静岡 3149 54.0
25 滋賀 3221 58.0
13 東京 4383 65.4 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
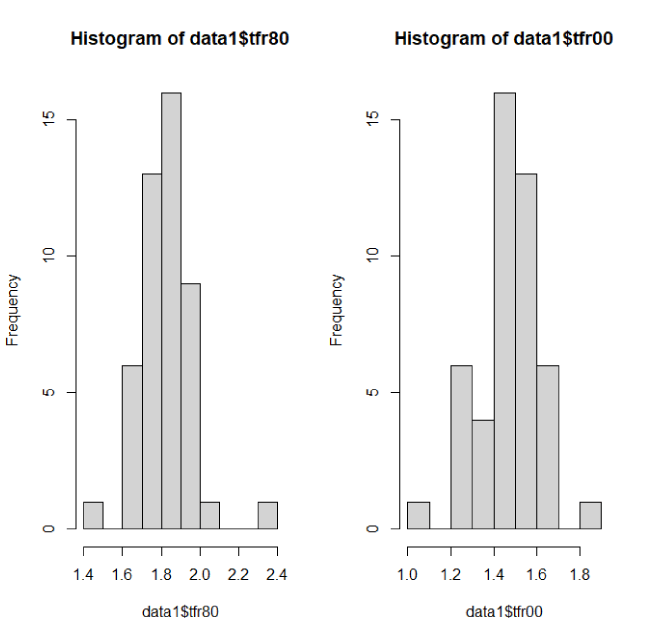
ヒストグラムの同時表示 デフォルトではヒストグラムは1つだけ出力されます。同時に表示したい時はparのmfrowで指定します。横に2つ(1行で2列)並べる場合は以下のとおりです。 > par(mfrow=c(1,2)) > hist(data1$tfr80) > hist(data1$tfr00)
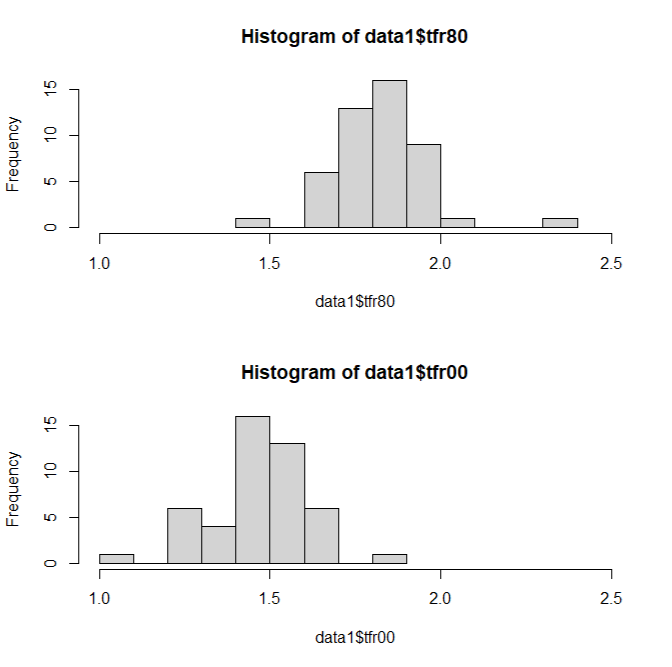
縦に2つ(2行で1列)並べたいときは以下のようにコマンドします。ここでは、横軸の幅をxlimを使ってそろえてみました。 > par(mfrow=c(2,1)) > hist(data1$tfr80, xlim=range(1.0,2.5)) > hist(data1$tfr00, xlim=range(1.0,2.5))
このグラフの並べ方の設定は継続しますので、元に戻したいときは以下を実行してください。 > par(mfrow=c(1,1)) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
基本統計量 データフレームを指定すると平均などが出ます。 標準偏差はでません。 > summary(data1) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
csvファイルの書き出し 変数の加工などでデータフレームに修正を加えた場合、保存する必要があります。一つの方法としてcsvファイルとして作業フォルダに書き出す命令があります。 以下は"data1"というデータフレームを"data2"というcsvファイルとして作業フォルダに書き出すコマンドです。 > write.csv(data1,file="data2.csv") ただ、このままだと行番号を一つの変数として認識してしまうので > write.csv(data1,file="data2.csv",row.names=FALSE) とします。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ダミー変数3 東京or三重ダミーの作り方。 都道府県が文字型変数の場合です。 > data1$tkymie <- data1$pref=="東 京 都" | data1$pref=="三 重 県" |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
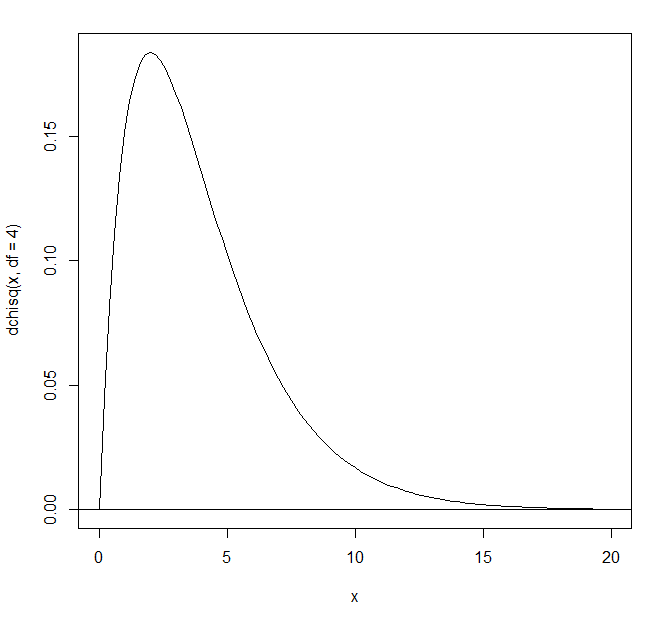
カイ2乗分布(自由度4) > curve(dchisq(x,df=4),xlim=c(0,20)) > abline(h=0) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
データの一部を使った回帰 データの一部を使って分析したい時があります。例えば以下のロング形式のパネルデータには1980年と2000年のデータがありますが、1980年のデータだけで回帰したり、あるいは2000年だけを使いたいとします。個票の分析では、男女別に推定したい場合もあるでしょう。 > data1
pref flp tfr year
1 北海道 47.1 1.64 1980
2 青森 53.5 1.85 1980
3 岩手 59.2 1.95 1980
(略)
45 宮崎 57.7 1.93 1980
46 鹿児島 50.8 1.95 1980
47 沖縄 46.4 2.38 1980
48 北海道 57.4 1.23 2000
49 青森 61.2 1.47 2000
50 岩手 63.4 1.56 2000
(略)
92 宮崎 62.9 1.62 2000
93 鹿児島 58.7 1.58 2000
94 沖縄 56.5 1.82 2000
2000年のデータを1、それ以外を0とするyearダミー(d00)を作成しておきます。これをしなくても、データの一部を使った回帰はできますが、後で散布図に示すために作成します。 > data1$d00 <- as.integer(data1$year==2000)
> data1
pref flp tfr year d00
1 北海道 47.1 1.64 1980 0
2 青森 53.5 1.85 1980 0
3 岩手 59.2 1.95 1980 0
(略)
45 宮崎 57.7 1.93 1980 0
46 鹿児島 50.8 1.95 1980 0
47 沖縄 46.4 2.38 1980 0
48 北海道 57.4 1.23 2000 1
49 青森 61.2 1.47 2000 1
50 岩手 63.4 1.56 2000 1
(略)
92 宮崎 62.9 1.62 2000 1
93 鹿児島 58.7 1.58 2000 1
94 沖縄 56.5 1.82 2000 1
全てのデータ、1980年データ、2000年データの順に推定してみます。subsetのところはyear変数で指定しても(例えばyear==2000)できます。 全て > attach(data1) > reg <- lm(tfr~flp) 1980年(d00=0) > reg1 <- lm(tfr~flp, subset=d00==0) 2000年(d00=1) > reg2 <- lm(tfr~flp, subset=d00==1) 推定結果は以下のとおりです。
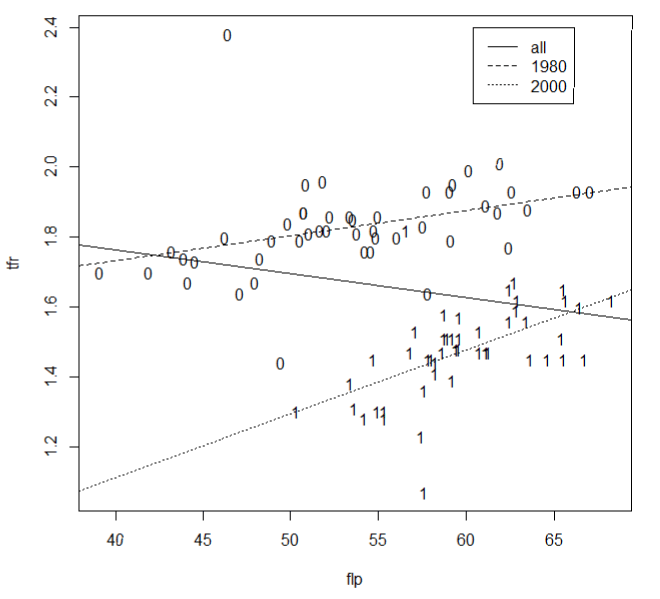
この結果を図に示します。plotとtextで1980年と2000年のデータをyearダミーの0、1で表示しています。ablineで推定された回帰直線を示していますが、ltyで線の種類を指定しています。最後にlegendで凡例を示していますが、locatorで任意の場所に表示できるようにしています。散布図の好きなところで左クリックして凡例を表示します。 > plot(flp,tfr,type="n")
> text(flp,tfr,d00)
> abline(reg,lty=1)
> abline(reg1,lty=2)
> abline(reg2,lty=3)
> legend(locator(1),c("all","1980","2000"),lty=c(1,2,3))
プールド回帰(全て)と単年回帰(1980年or2000年)の傾きの違いが視認できます。
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ダミー変数2 講義用データ"panel"を使用します。 > data <- read.csv("panel.csv")
> attach(data)
2000年のデータを1、それ以外を0とするダミー変数の作成方法は以下のようにしますが、こうするとTRUE、FALSEという表示になります。推定では1,0として扱われますが。 > data$d00 <- year==2000 データ上でも1,0表示にしたければ以下のようにコマンドします。 > data$d00 <- as.integer(year==2000) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
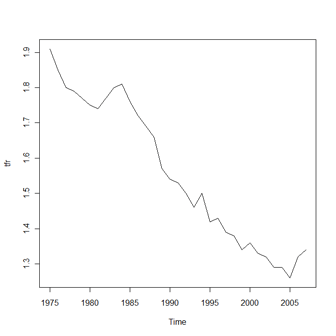
時系列データ データフレーム(data1)にある変数(tfr)を1975年スタート、1年ごとの時系列データとして認識させます。 > tfr <- ts(data1$tfr,start=c(1975),frequency=1) データを表示すると > tfr Time Series: Start = 1975 End = 2007 Frequency = 1 [1] 1.91 1.85 1.80 1.79 1.77 1.75 1.74 1.77 1.80 1.81 1.76 1.72 1.69 1.66 [15] 1.57 1.54 1.53 1.50 1.46 1.50 1.42 1.43 1.39 1.38 1.34 1.36 1.33 1.32 [29] 1.29 1.29 1.26 1.32 1.34 のようになります。また、以下のコマンドで時系列プロットができるようになります。 > plot(tfr)
さらに1階の階差をとるコマンドはdiff( )です。 > tfr_d1 <- diff(tfr) 以下のようにデータが作成されます。 > tfr_d1 Time Series: Start = 1976 End = 2007 Frequency = 1 [1] -0.06 -0.05 -0.01 -0.02 -0.02 -0.01 0.03 0.03 0.01 -0.05 -0.04 -0.03 [13] -0.03 -0.09 -0.03 -0.01 -0.03 -0.04 0.04 -0.08 0.01 -0.04 -0.01 -0.04 [25] 0.02 -0.03 -0.01 -0.03 0.00 -0.03 0.06 0.02 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
交差項を使った回帰 交差項をデータとしてあらかじめ作成する必要はなく、式に記述すればOK。 reg1 <- lm(Y~x1+x2+x1*x2) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
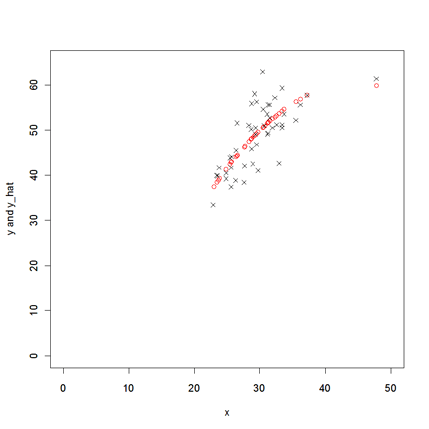
実現値と予測値のプロット 実現値yと回帰(ols6)による予測値y_hatを散布図にプロットする。 > plot(Inc05r,predict.lm(ols6),ylim=c(0,65),xlim=c(0,50),col=2,xlab="x",ylab="y and y_hat") > par(new=T) > plot(Inc05r,sch06,ylim=c(0,65),xlim=c(0,50),pch=4,xlab="",ylab="")
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
系列相関の検定 パッケージlmtestをDLしてインストールしておく。ここでは推定結果がols1に格納されているものとします。 > dwtest(ols1) 不均一分散のテスト 同じくlmtestがインストールされていれば実行可能。 > bptest(ols1) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
recode 最終学歴(1:中学、2:高校、3:短大・高専、4:大学・大学院)を修学年数(9:中学、12:高校、14:短大・高専、16:大学・大学院)にリコードする。 > library(car) > data1$yedu=recode(edu,'1=9;2=12;3=14;4=16') |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
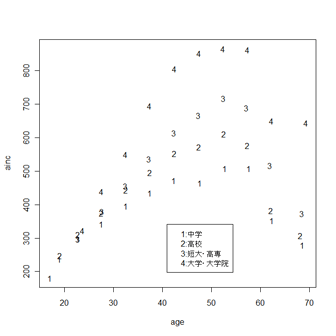
散布図の凡例表示
学歴(edu)別に年齢(age)と年収(ainc)の対応をプロットする。 > plot(age,ainc,type="n") > text(age,ainc,edu) そのあと > legend(locator(1),c("1:中学","2:高校","3:短大・高専","4:大学・大学院")) を実行してグラフの任意の場所に左クリックで凡例を表示する。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
一部の変数で別のデータフレームを作成 data1にいろいろな変数がある場合、以下のようにして抜き出すことができます。 > attach(data1) > data2 <- data.frame(inc05,stu05,unv05) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
残差プロット 時系列データの分析で、残差を時系列でプロットします。ols1に推定結果が格納されています。 > plot(year,residuals.lm(ols1)) また、以下のように予測値を計算して実現値から引いてもできます。 > data1$ptfr <- predict(ols1) > data1$res <- tfr-ptfr > attach(data1) > plot(year,res) > abline(h=0) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
定数項なしの回帰 階差データの回帰などで定数項なしで回帰したいときがあります。その場合、式の部分に「0」と記述すればOKです。 > ols1 <- lm(tfr~0+uem) また、「1」と記述すれば、通常の定数項ありの回帰になります。 > ols2 <- lm(tfr~1+uem) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| read.csv("外部ファイル名.csv")
> read.table("外部ファイル名.csv",header=TRUE,sep=",") で外部データを読み込めますが、 > read.csv() ではheader以降の部分を省略することができます。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| edit(データフレーム名) データエディタを開きます。データを直接、修正することができます。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 分散
不偏分散を求めるコマンドはvar(x1)です。標本分散を求めるには以下のどちらかでどうぞ。 > var(x1)*(length(x1)-1)/length(x1) > sum((x1-mean(x1))^2)/(length(x1)) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
t分布のグラフ
以下のコマンドで作成しました。もっとシンプルなものもあると思うのですがとりあえず。 > curve(dt(x,45),-5,5,xlab="t") > abline(h=0) > segments(qt(0.025,45),0,qt(0.025,45),dt(qt(0.025,45),45));segments(qt(0.975,45),0,qt(0.975,45), dt(qt(0.975,45),45)) > segments(qt(0.005,45),0,qt(0.005,45),dt(qt(0.005,45),45));segments(qt(0.995,45),0,qt(0.995,45), dt(qt(0.995,45),45)) > text(0, 0.05, labels="95%") > arrows(-0.6, 0.05,qt(0.025,45),0.05);arrows(0.6,0.05,qt(0.975,45),0.05) > text(0,0.01,labels="99%") > arrows(-0.6,0.01,qt(0.005,45),0.01);arrows(0.6,0.01,qt(0.995,45),0.01) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
データの接合 data1とdata2を変数prefで一致するように接合し、新たなdata3としています。 > data3 <- merge(data1,data2,by="pref",all=TRUE) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 相関係数の有意性検定
2つの変数x1とx2の相関係数の有意性検定を行います。 > cor.test(x1,x2) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 偏相関係数
偏相関係数のコマンドが見当たらないので関数作成の練習として示しておきます。 3変数x、y、zがあったとき、zの影響をコントロールした後のxとyの偏相関係数は以下の関数で求められます。 > pcor <- function(x,y,z){
> rxy <- cor(x,y)
> rxz <- cor(x,z)
> ryz <- cor(y,z)
> rxyz <- (rxy-rxz*ryz)/((sqrt(1-(rxz)^2))*(sqrt(1-(ryz)^2)))
> rxyz
> }
と打ち込んで実行したらx、y、zに変数を指定します。都道府県データinc、enr、univがあり、univの影響をコントロールした場合のincとenrの偏相関係数について計算すると > attach(data1) > pcor(inc,enr,univ) [1] 0.6897585 となります。この偏相関係数について有意性の検定をするときは、まずt値を計算します。 > pcor(inc,enr,univ)*sqrt(47-1-2)/sqrt(1-pcor(inc,enr,univ)^2) [1] 6.319187 自由度44の両側10%点は > qt(0.95,44) [1] 1.68023 となるので、10%水準の境界値を超えていることがわかります。p値を求めると > 2*pt(6.319187,44,lower.tail=FALSE) [1] 1.144776e-07 となり、十分に低い値になっていることがわかります。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ダミー変数1
東京ダミーの作り方。 都道府県が文字列型の場合 > data6$tokyo <- data6$pref=="東 京 都" 都道府県が数値型の場合 > data6$tokyo <- data6$pref==13 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 相関行列
データフレームdata1にあるすべての変数間の相関係数を行列形式で出力する。 > cor(data1) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| attach(データフレーム名)
> attach(data1) としておくと、以下のようにデータフレームの指定を省略できます。 > ols1 <- lm(sch06~inc05+stu05+unv05) ただし、新たな変数をデータフレームに追加した時は、再度attachするのを忘れないようにしましょう。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||